Analýza prostorových dat metodou
prostoro-časového shlukování a testování přítomnosti shluků kolem bodového
zdroje
Jana
Možiešiková
Institut ekonomiky a systémů řízení
VŠB – Technická univerzita Ostrava
tř. 17. listopadu
708 33 Ostrava – Poruba
E-mail: janamo@email.cz
Abstrakt
Cílem této diplomové práce bylo nalézt vhodný způsob pro výpočet prostoro-časových shlukování. Jejím úkolem bylo vyzkoušet některé metody a odhalit jejich potenciál pro takováto studia.
Úvod práce je věnován seznámení s některými přístupy ke zpracování bodově lokalizovaných událostí a metod analýzy prostoro-časového shlukování. Zvláštní pozornost je věnována problematice získávání a úpravy dat.
Další část práce se zabývá popisem nalezených vhodných programů, které umožňují mimo jiné výpočet prostoro-časových shluků.
Poté následuje popis vlastní tvorby programových aplikací pomocí ArcView 3.2 v jeho vývojovém prostředí Avenue. Tato část obsahuje také ukázky výsledných tabulek a obrázků. Vše je detailně popsáno.
Závěrečná část se věnuje vizualizaci výsledků nejen v podobě mapových kompozic a celkovému zhodnocení dosažených výsledků.
Prostoro-časové shlukování
Při studiu prostoro-časového shlukování se analyticky testuje, zda dochází ke shlukování pozorovaných událostí v prostoru za určité časové období. Takže cílem prostoro-časového shlukování je posoudit, zda dochází u pozorovaných událostí současně ke shlukování v čase a v prostoru, zda platí korelace mezi vzdáleností v prostoru a časovým rozdílem v čase konání jednotlivé událostí. Zajímá nás také, zda prostor a čas na sebe nějakým způsobem navzájem působí.
Tento způsob je v praxi využíván především pro studium dynamických procesů v oboru epidemiologie.
Testy vhodné pro zjištění prostoro-časového
shlukování
Knoxův test
Z n událostí je možno získat n*(n-1) uspořádaných párů (srovnávání a porovnávání dvojic). Knoxův test je založen na porovnání pravděpodobnosti p(x) pro výskyt událostí blízkých v prostoru i v čase.
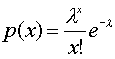
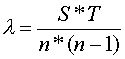
Je-li hodnota p(x) „příliš malá“, nelze jev považovat za náhodný a musíme
odmítnout nezávislost tvorby shluků v čase a prostoru.
K-funkce
Je-li R plocha oblasti r, pak očekávaný počet událostí v r je l*R. Z definice K-funkce plyne, že očekávaný počet uspořádaných párů událostí ve vzdálenosti do h je l2*R*K(h). Je-li dij vzdálenost mezi i-tou a j-tou pozorovanou událostí v r a Ih(dij ) je indikátorovou funkcí, která nabývá hodnoty 1, pokud je dij £ h, a hodnoty 0 pro opačný případ, pak pozorovaný počet uspořádaných párů je åi¹j å Ih (dij ). Proto vhodným odhadem K(h) bude:
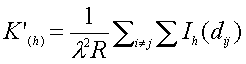
Test pro prostoro-časové vztahy může být založen na pozorovaných rozdílech K funkcí:
D‘(h,t)=K‘(h,t)-K‘S(h)K‘T(t)
Nepřímo standardizovaná incidence
Metoda nepřímo standardizované incidence je jednou z nejčastěji používaných standardizačních metod v epidemiologii. Výskyt nádorových onemocnění v každém územním celku je charakterizován veličinou, která eliminuje rozdíly ve věkovém složení. SIR díky tomu ukazuje, jaký by byl očekávaný výskyt nádorových onemocnění v každém ze studovaných územních celků, kdyby frekvence výskytu v této populaci byla stejná, jako ve standardu ČR. SIR je pak procentuálním vyjádřením poměru skutečného a očekávaného počtu onemocnění ve studované populaci. Hodnoty SIR pohybující se kolem hodnoty 1 tak charakterizují průměrný výskyt nádorových onemocnění, hodnoty nízkého výskytu onemocnění charakterizuje SIR < 1 a naopak, SIR>1 charakterizuje nadprůměrnou incidenci.
Hodnotu SIR lze vypočítat jako podíl skutečného počtu nových případů ku očekávanému počtu případů. Očekávaný počet nových případů je vypočten aplikací standardní relativní incidence (standart age specific rate) na jednotlivé populační skupiny.
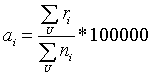
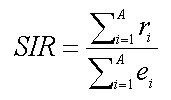
![]()
Použité datové zdroje
· Ročenka ústavu pro zdravotnické informace (ÚZIS)
· Datová sada ArcČR 500
· Data z NOR (Národní onkologický registr) – severní Morava
· SLDB91 – data ze sčítání lidu z roku 1991
Tvorba aplikací pomocí Avenue (implementace do ArcView)
Byly vytvořeny 4 aplikace: a. výpočet reprezentativních bodů invariantních skupin obcí
b. výpočet SIR
c. výpočet Knoxova testu
d. výpočet K funkce
ad c.
Aplikace
počítá prostorové vzdálenosti i časové intervaly.
Výpočet prostorové
vzdálenosti
Zde je porovnávána každá událost s každou, v takovém pořadí v jakém jsou uspořádány v tabulce událostí (analyzas.dbf). Tak jako u výpočtu SIR, kde se počítalo se souřadnicemi reprezentačních bodů obcí, které měly stejným kódem „S“, stejně tak se počítalo s tímto reprezentačním bodem i u tohoto testu. Zjišťovaly se vzdálenosti (v metrech) mezi jednotlivými reprezentačními body obcí.
![]()
Výpočet časového intervalu
Každé události byl, jak už bylo zmíněno, přidělen jedinečný identifikátor. Porovnávání všech událostí bylo provedeno obdobně jako u prostorové vzdálenosti.
rok diagnózy jedné události
– rok diagnózy jiné události = časový interval
Zvolení
vhodných intervalů
U Knoxova testu, jak již bylo dříve zmiňováno, je nutné zvolit v závislosti na datech limity pro prostor i pro čas (S, T).
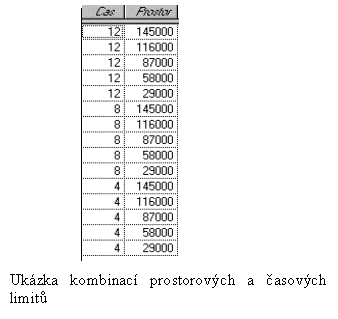
V tomto případě byly prostorové a časové intervaly voleny takto:
Celkové období sledování diagnózy nemoci je od roku 1977 do 1999, takže 23 let. Toto období bylo rozděleno celkem do 6 intervalů po 4 letech .
Obdobně byly zvoleny i prostorové intervaly. Nejprve byla zjištěna největší vzdálenost mezi obcemi a ta byla, stejně jako v časovém intervalu, rozdělena do 6 intervalů přibližně stejných.
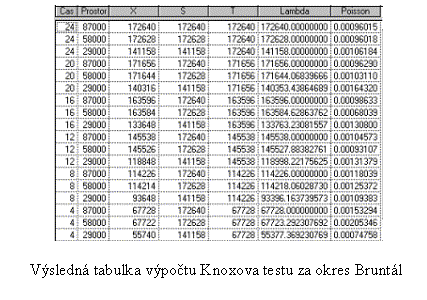
Výsledek
zpracování Knoxova testu
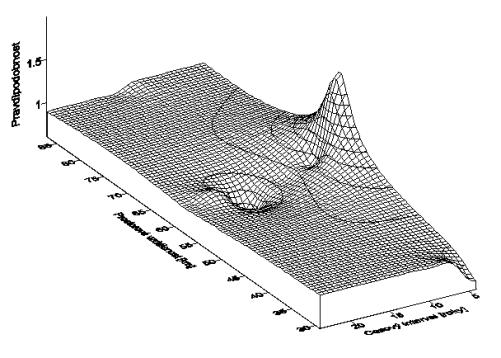
Povrchový graf
znázorňující výsledky Knoxova testu za okres Bruntál
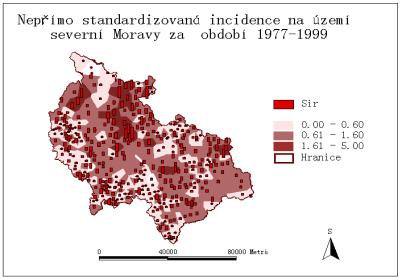
Jeden
z výstupů výpočtu Nepřímo standardizované incidence
Použitá literatura
[1] Bailey, T.C., Gatrell, A.C., „Interactive
spatial data analysis“ Essex, Longman Scientific &
Technical, 1995
[2] Eliot, P., Englist, D., Steam, R.,:
Geographical & Environmental Epidemiology
[3] Maršík, V., a kol.,: Atlas výskytu zhoubných nádorů v České republice 1978-1994, Masarykův onkologický ústav v Brně, Brno 1998
[4] Mantel, N.,: The detection of disease
clustering and a generalised regression approach, Cancer Research, 1967
[5] Horák, J.: Úvod do prostorové analýzy dat, učební texty, Ostrava 1998
[6] Kaňok, J.: Tematická kartografie, Ostrava 1999
[7] www.ai-geostats.org